correspondances entre les planètes et les notes de musique
Rédigé en 2019
Il ne s’agit pas ici de disserter sur ce que les Anciens désignaient sous le nom d’« harmonie des sphères », mais seulement de mentionner une correspondance réelle et précise entre les orbites des planètes du système solaire, et les fréquences des notes de musiques.
Les orbites sont mesurées ici par les demi-grands axes des ellipses de révolution des planètes autour du Soleil. On pourrait prendre aussi les périmètres de ces ellipses ; à vrai dire, ces ellipses sont pratiquement des cercles, du fait que leurs excentricités sont toutes très petites. Donc cela revient au même.
Aux planètes habituelles, nous avons ajouté les 2 plus grandes des « petites planètes » : Cérès et Pluton.
Les notes sont mesurées par les différences entre leur longueur d’onde et celle d’une note de référence.
On est amené à distinguer les planètes proches du Soleil, petites (Mercure, Vénus, Terre, Mars, Cérès) ; et les planètes lointaines (Jupiter, Saturne, Uranus, Neptune, Pluton), très grandes sauf Pluton.
Les correspondances sont les suivantes, pour les planètes proches, et lointaines :
Soleil: do; Mercure: do #; Vénus: ré; Terre: mi b; Mars: fa; (Cérès: si b)
(Pluton: si b); Neptune: do; Uranus: ré; Saturne: mi b; Jupiter: fa; Soleil: sol b
Elles sont très précises, comme le montre la note de calcul (voir ci-dessous), et ne peuvent donc pas être attribuées au hasard. Alors :
Selon Pythagore, « tout est nombre », les nombres sont le principe de l’harmonie universelle.
Il n’y a pas de hasard ; comme disait Einstein, « Dieu ne joue pas aux dés ».
Ou encore: « ce qui est en haut est comme ce qui est en bas ».
Et faut-il s’en étonner ? Probablement pas : des planètes dont les orbites seraient aléatoires ne pourraient pas former un système (relativement) stable, sans doute, étant donné les interactions possibles entre les forces de gravitation. Mais je ne saurais en dire plus, je ne suis pas astrophysicien.
__________________________________________________________________________________
Correspondance entre planètes et notes de musique : note de calculs
On compare les deux séries de valeurs :
- les demi grands axes des orbites des planètes,
- avec les différences entre la longueur d’onde de la note et celle d’une note de référence.
Le choix de la note de référence importe peu, puisque c’est une question de rapports. Prenons par exemple do 3 (dans l’air avec vitesse du son 340 m/s, do 3 a une fréquence de 523 Hz, longueur d’onde 0.650 m).
On calcule la régression linéaire entre ces deux séries de valeurs. La précision de la régression est mesurée par l’écart-type de la différence entre la note réelle et la droite de régression.
Calculs et figures ci-dessous sont effectués avec le logiciel de calcul « scilab » (ce logiciel est à la fois gratuit et efficace, donc il mérite d’être cité. Un habitué du logiciel professionnel « matlab » – très cher – l’utilise avec aisance).
Il est correct de tenir compte du fait qu’il y a plusieurs gammes (avec des rapports de fréquences légèrement différents d’une gamme à l’autre). On prend donc en compte les principaux types de gamme connus en Europe :
- tempérée,
- pythagoricienne,
- et « naturelle » – ou du moins l’une des gammes naturelles ; ici avec les rapports à la tonique (do) présentés dans le tableau ci-dessous :
| Do # | Ré | Mi b | Fa | Sol b | Si b |
| 17/16 | 9/8 | 6/5 | 4/3 | 25/18 | 16/9 |
Petites planètes
Les séries de valeurs sont listées dans le tableau ci-dessous :
A : demi grand axe, en « unité astronomique » (c.a.d. rapporté à celui de la Terre)
L : différence de longueur d’onde, en cm.
| Planète | Soleil | Mercure | Vénus | Terre | Mars | Cérès |
| A | 0 | 0.387 | 0.723 | 1 | 1.524 | 2.767 |
| Note | Do | Do # | Ré | Mi b | Fa | Si b |
| L, gamme tempérée | 0 | 3.65 | 7.09 | 10.34 | 16.30 | 28.51 |
| L, gamme « naturelle » | 0 | 3.82 | 7.22 | 10.83 | 16.24 | 28.43 |
| L, gamme « pythagoricienne » | 0 | 4.13 | 7.22 | 10.89 | 16.90 | 28.92 |
Deux régressions linéaires sont représentées dans la figure ci-dessous, l’une sans, l’autre avec Cérès.
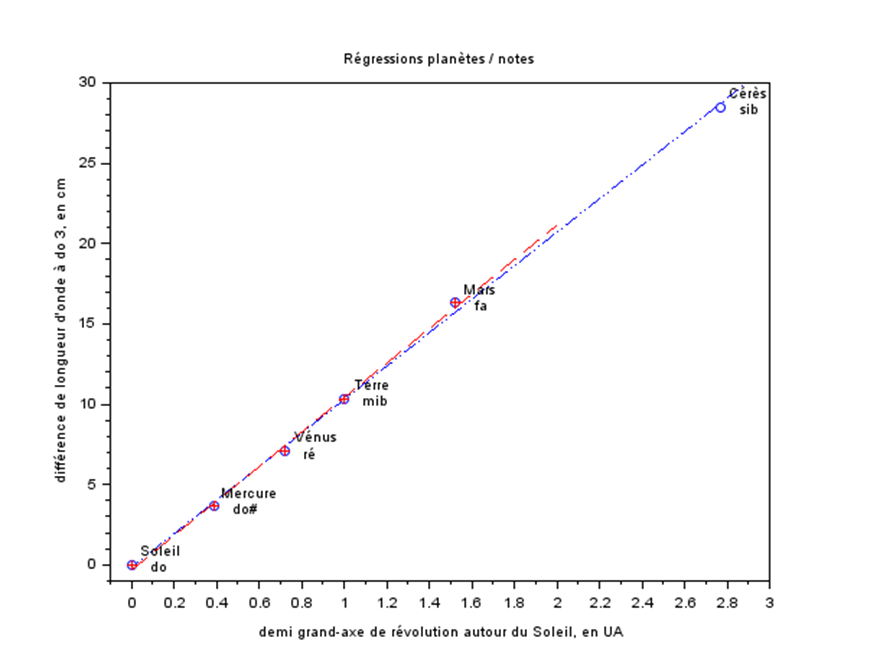
Les précisions des régressions linéaires sont notées dans le tableau ci-dessous :
| gamme | tempérée | « naturelle » | pythagoricienne |
| Erreur moyenne, sans Cérès (cm) | 0.26 | 0.23 | 0.29 |
| Id., avec Cérès | 0.29 | 0.31 | 0.41 |
On calcule aussi les régressions des gammes les unes entre elles : ainsi pour la corrélation entre gammes tempérée et naturelle, l’erreur moyenne 0.19 cm (0.18 cm sans le si b)
Pythagoricienne / naturelle : 0.19 cm
Grandes planètes
Séries de valeurs :
| Planète | Pluton | Neptune | Uranus | Saturne | Jupiter | Soleil |
| A, UA | 39.48 | 30.07 | 19.19 | 9.54 | 5.20 | 0 |
| Note | Si b | Do | Ré | Mi b | Fa | Sol b |
| L, gamme tempérée | -7.96 | 0 | 7.09 | 10.34 | 16.30 | 18.19 |
Graphique des régressions linéaires, sans, et avec Pluton :
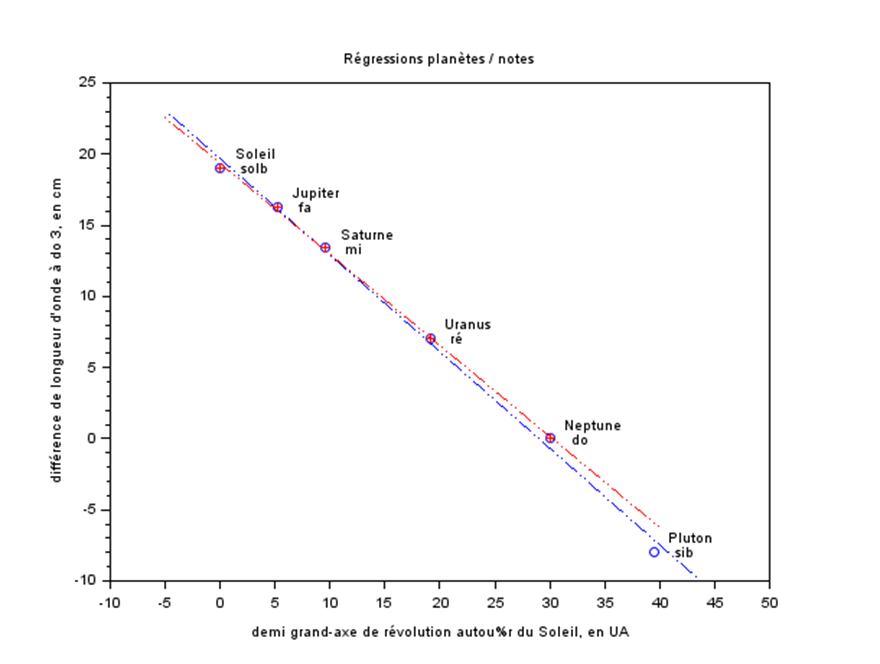
Précisions des régressons :
| gamme | tempérée | « naturelle » | pythagoricienne |
| Erreur moyenne, sans Pluton (cm) | 0.21 | 0.43 | 0.31 |
| Id., avec Pluton | 0.57 | 1.05 | 0.40 |
Régressions des gammes entre elles :
Tempérée / naturelle : 0.49 cm ; 0.25 cm sans si b
Pythagoricienne / naturelle : 0.27 cm ; 0.12 cm sans si b.
Observations principales :
A vue d’œil sur les figures, les corrélations sont toutes excellentes.
Elles sont un peu moins bonnes si on prend en compte les « petites planètes » Cérès et surtout Pluton. Planètes que les astronomes hésitent d’ailleurs à considérer comme telles.
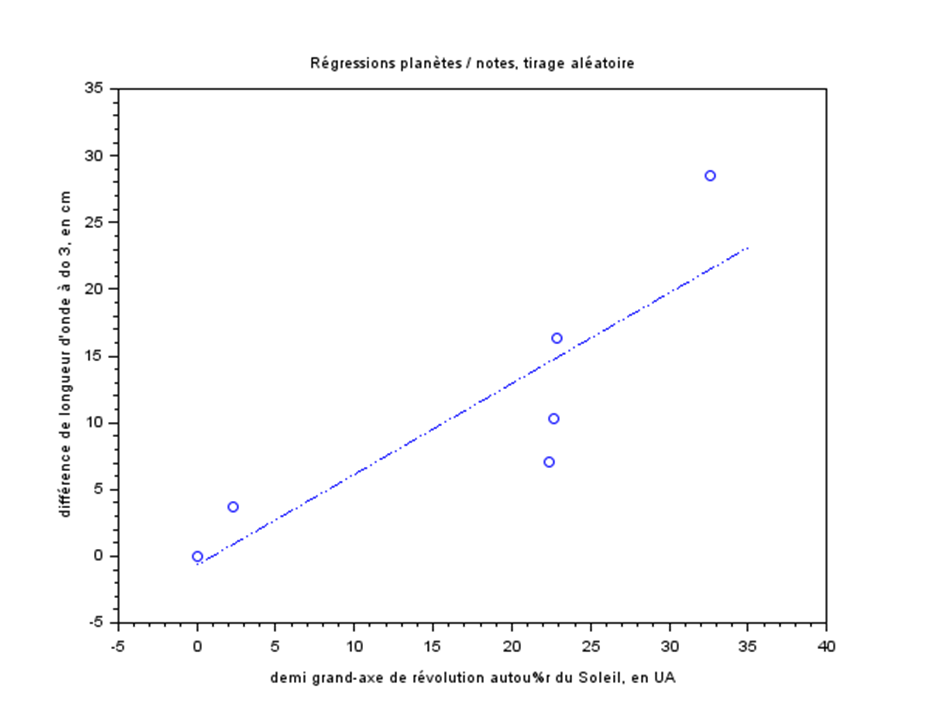
Pour s’en assurer mieux, il convient de voir la régression obtenue avec un tirage aléatoire. Prenons par exemple le cas des planètes proches. La série des grands axes des planètes étant donnée, on effectue un tirage aléatoire des longueurs d’onde, que l’on range par ordre croissant.
La figure ci-dessous en montre un exemple.
L’erreur moyenne calculée sur un grand nombre de tirages est de 3.4 cm, soit plus de 10 fois les erreurs obtenues avec les notes réelles.
Il faut surtout remarquer que l’erreur moyenne des régressions entre les diverses gammes est à peine inférieure à celles des régressions entre les planètes et l’une ou l’autre de ces gammes. Ce qui confirme que cette dernière est vraiment négligeable. CQFD.